Quantum State Engineering 101
Or: Make Pure Quantum States of Light With This One Weird Trick*
November 26, 2014In my past life, I worked as a quantum mechanic in Paul Kwiat’s group at the University of Illinois, where we shoot crystals with lasers and do fun things with photons. In this post I’m going to tell you a bit about my research on producing photons in pure quantum states. I hope anyone with any level of background can get something out of this, but it will help if you know what a photon is, and a little bit about quantum mechanics.
There are many reasons why we might want to produce pure quantum states: for technologies like quantum computing, quantum cryptography and quantum teleportation, or just to better understand the universe. But what do we mean by a pure state?



Tools of the trade: lenses, mirrors, lasers, and prisms
Purity and Indistinguishability
First I’ll introduce the concept of polarization. Simply put, if light is a wave, polarization describes the direction it’s waving in. For example, side-to-side (\(H\), horizontal), or up-and-down (\(V\), vertical). However, we’re not just restricted to one polarization or the other: we can also have a superposition state of both at the same time,1 \(\frac{H+V}{\sqrt{2}}\). But this is not the only way to have both \(H\) and \(V\): we could also have a random number generator that flips a switch, choosing to generate \(H\) photons half the time and \(V\) photons half the time. This is the critical distinction of a pure state: \(H\), \(V\), and \(\frac{H+V}{\sqrt{2}}\) are all pure, while a random selection of \(H\) or \(V\) is a classical statistical mixture, or mixed state. Put another way, with both the superposition state and mixed state, we can make a measurement that asks: “are you \(H\) or \(V\)”, and have a chance to get either answer. However, in the (pure) superposition state, the photons that end up being \(H\) or \(V\) are actually identical up until the measurement is made, while in the mixed state they are not.
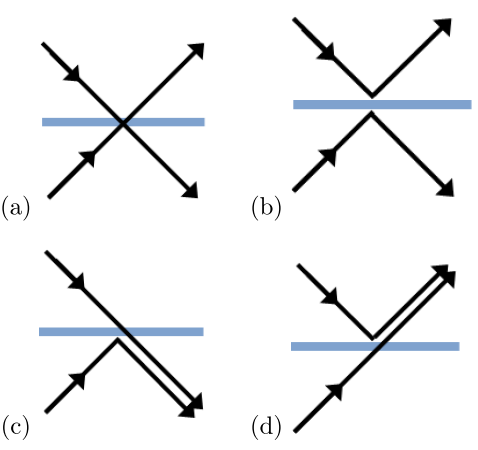
Four possibilities for two single-photons interacting with a beamsplitter
This implies that purity is closely related to indistinguishability. In quantum mechanics, all particles of the same species are all capable of being indistinguishable. If two photons are prepared in the exact same pure state, there is no way to tell them apart or assign different labels to each photon. However, if the photons have, say, a different amount of energy, we can use this property to distinguish them. We can quantify this through the Hong-Ou-Mandel effect. Suppose we direct a single photon to a 50/50 beamsplitter. There are two possibilities: 50% of the time the photon will be reflected, and 50% of the time it will be transmitted. Now, if we send a second photon to the other side of the beamsplitter, we have four possibilities, diagrammed to the right: (a) both transmitted, (b) both reflected, and (c,d) one transmitted, one reflected. According to quantum mechanics, to determine the outcome of an experiment, we have to add the probability amplitudes for all possible indistinguishable processes. In this example, (a) and (b) have identical outcomes but opposite2 probability amplitudes: these terms cancel (much like destructive interference of classical waves) and the photons will always exit the beamsplitter together, as in (c) and (d)! However, if the photons are not identical and indistinguishable, the amplitudes are not added, and we will observe outcome (a) or (b) half the time. To make the connection to purity explicit, if the quantum state is not pure, then the photons are a statistical mixture of different states and we cannot guarantee they are actually identical.
Photon Pairs
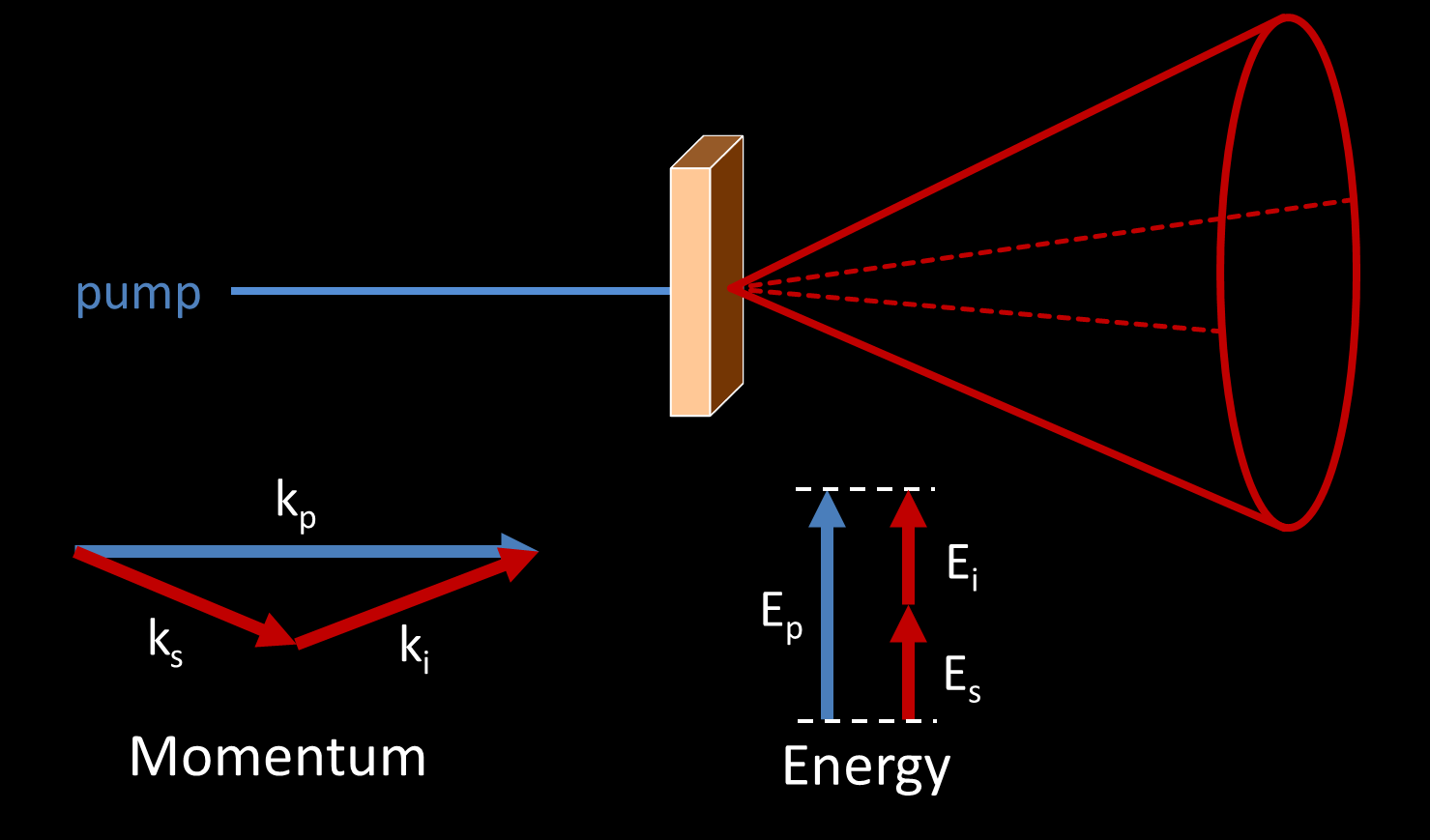
Energy and momentum conservation in Type-I spontaneous parametric downconversion
Until now, I’ve completely left out how we can actually produce single photons to begin with! This turns out to be rather difficult, but it can be done with a few techniques. The most widely-used of these is spontaneous parametric downconversion (SPDC).3 In SPDC, a “pump” photon (usually from a laser) passing through a nonlinear optical crystal has a small chance to downconvert into a pair of daughter photons (“signal” photon \(s\) and “idler” photon \(i\)).
Energy and momentum are conserved, so the energies and momenta of the daughter photons have to add up to the original energy and momentum of the pump photon. These conservation constraints lead to an important property: the two daughter photons are always produced on opposite sides of an imaginary cone. Thus, if we detect one of them, we know exactly where to find its sibling even before we look for it! This implied sibling is known as a heralded single photon, and is the starting point for many quantum information experiments.
The tricky part comes in when we want this heralded single photon to be in a pure state, for example to interfere with another photon (like in the Hong-Ou-Mandel effect example above). If there are correlations between the photons in the pair, the heralded photon will actually be in a mixed state. One typical way this occurs is through conservation of energy: the constraint that \(E_{p} = E_{s} + E_{i}\) (recall that the energy of a photon is related to its wavelength by \(E=hc/\lambda\), where \(h\) is Planck’s constant and \(c\) is the speed of light) implies that if we know the energy of the pump and the signal photons, we can precisely guess the the energy of the idler photon. If these energies vary from pair to pair, this leads to a mixed state!
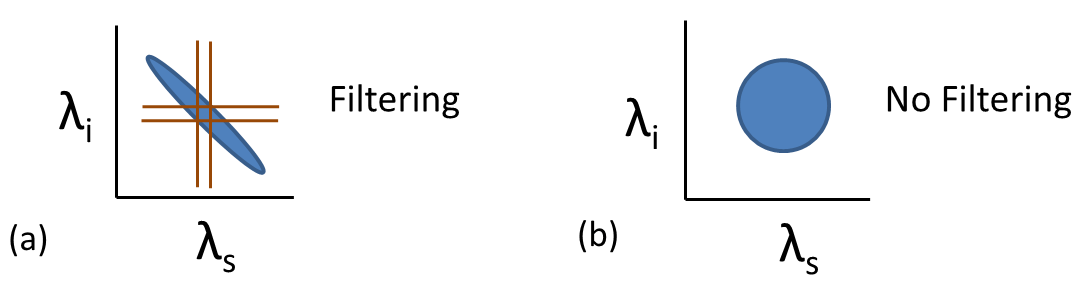
Joint spectral distribution as a function of signal wavelength and idler wavelength. (a) Filtered, correlated joint spectrum. (b) Uncorrelated joint spectrum, no filtering needed.
We can avoid this in two ways: (a) use narrow filters that only allow photons with a very specific energy to pass, or (b) engineer the quantum state itself by using pump photons with a lot of energy uncertainty (broad bandwidth and ultrafast pulses, as short as 35 femtoseconds!). We can visualize both of these options by plotting the joint spectrum, which is a two-photon probability density.4 If the joint spectrum is conditionally independent (for example, circular), a measurement of one photon yields no information about its sibling, and no correlations are present. This is the criteria for heralded pure states. Conservation of momentum also leads to correlations, which I’ll discuss in the next section.
The goal of quantum state engineering is to achieve option (b)! While this is difficult both theoretically and in practice, the logic of it is simple: narrow filters throw out most of the photons that we generate, so if we don’t have to use them, we can collect many more photons. This has a potentially enormous impact for the speed of protocols like quantum teleportation that use these photons as a resource.

Lots of optics go in to engineering and collecting photon pairs. This photo shows some of the lenses, crystals, and mounts used for pair collection.
Phase-matching
I’ve kept the math under the rug until this section. Feel free to skip to the next section if you don’t want to see the gory details!
To engineer a source of factorable photons, one must calculate the dependence of frequency and spatial correlations on the physical parameters of the SPDC scheme. The state produced by SPDC can be expressed in terms of creation operators, the signal and idler wavevectors \(\vec{k}_{s}\) and \(\vec{k}_{i}\), and a constant \(\eta\) as
\[\left|\psi\right\rangle =\left|\textrm{vac}\right\rangle +\eta\int d\vec{k}_{s}\int d\vec{k}_{i}F(\vec{k}_{s},\vec{k}_{i})\hat{a}_{s}^{\dagger}(\vec{k}_{s})\hat{a}_{i}^{\dagger}(\vec{k}_{i})\left|\textrm{vac}\right\rangle .\]Here, \(F\) is the joint two-photon amplitude (JTPA), which can be written as
\[F(\vec{k}_{s},\vec{k}_{i})=\ell(\vec{k}_{s})\ell(\vec{k}_{i})\alpha(\omega_{s}+\omega_{i})\phi(\vec{k}_{s},\vec{k}_{i}),\]where \(\ell(\vec{k}_{s})\) and \(\ell(\vec{k}_{i})\) are separable terms, \(\alpha\) is the pump spectral amplitude (assumed to be Gaussian), and \(\phi\) is the phase-matching function. Ideally, all the terms in the JTPA would be separable, so we could write \(F(\vec{k}_{s},\vec{k}_{i})=S(\vec{k}_{s})I(\vec{k}_{i})\) for some functions $S$ and $I$ which depend only on the signal and idler photons, respectively. If this were the case, there would be no correlations between the signal and idler photons, the source would be factorable, and each photon would individually be in a pure state. Unfortunately, \(\alpha\) and \(\phi\) are not in general separable. However, by adjusting the appropriate parameters of the system, these terms can be made approximately separable. To see how, we consider the full form of the phase-matching function, annotated below:
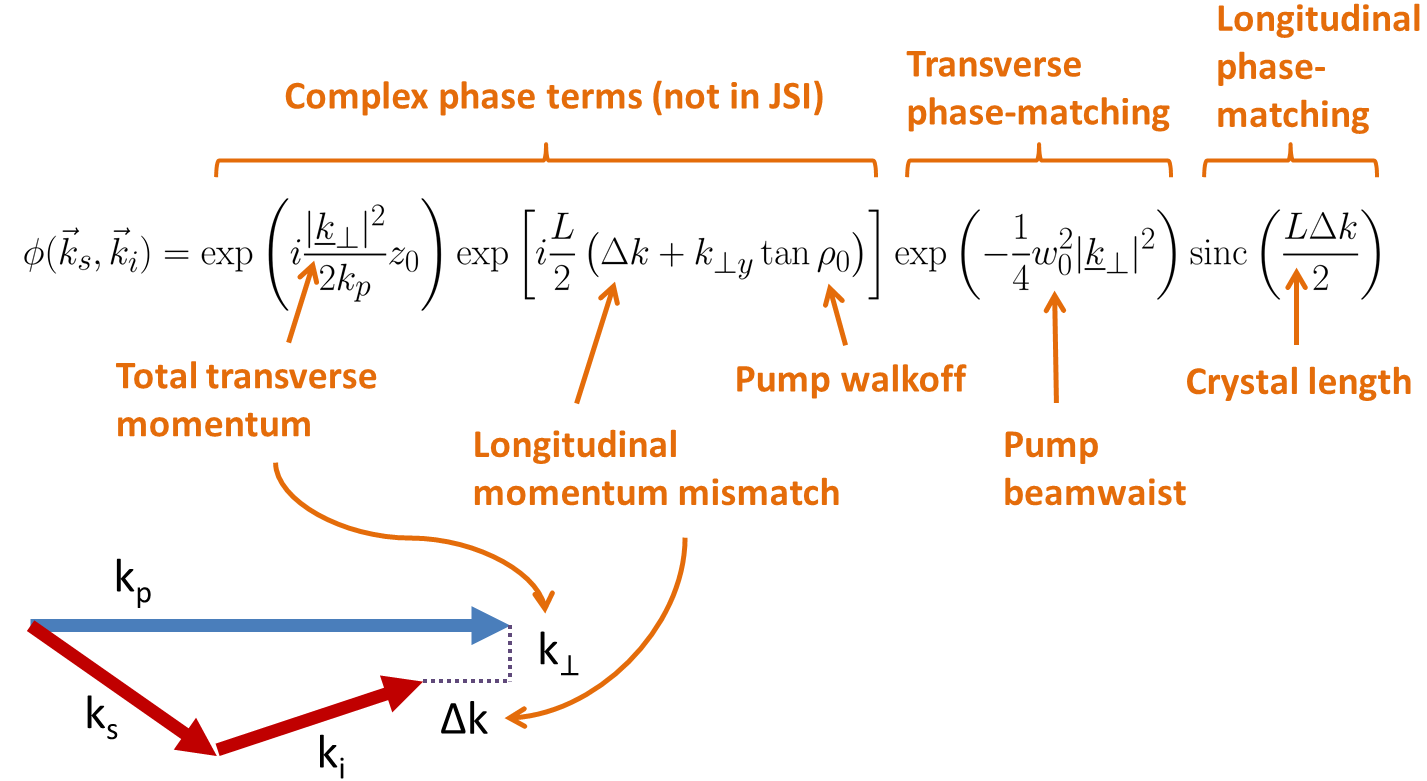
Annotated phase-matching function.
Transforming \(\phi(\vec{k}_{s},\vec{k}_{i})\) into spherical coordinates \(\{\omega_{s},\theta_{s},\phi_{s},\omega_{i},\theta_{i},\phi_{i}\}\) and Taylor-expanding to first order provides of a set of constraints to satisfy in order for non-separable cross terms to vanish, and thus for the source to be factorable. Roughly stated, the criteria are:
- Choosing the collection angles \(\theta_{s}\) and \(\theta_{i}\) so the longitudinal component of the signal and idler group velocities match the pump group velocity.
- Selecting the pump beam waist and crystal length according to the collection angles.
- Using a pump bandwidth larger than a threshold value which is inversely proportional to crystal length.
- Collecting photons in a small angular spread around \(\theta_{s}\) and \(\theta_{i}\).
The conservation constraints of the pump envelope and phase-matching function are animated below, demonstrating how a nearly separable joint spectrum can be obtained by appropriate selection of source parameters.
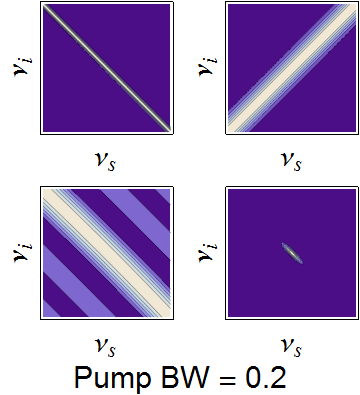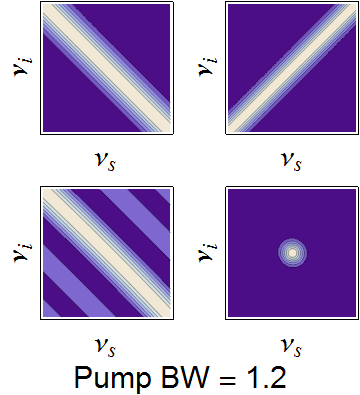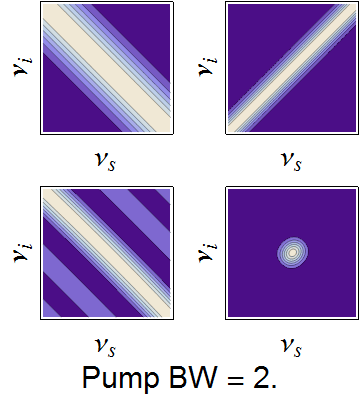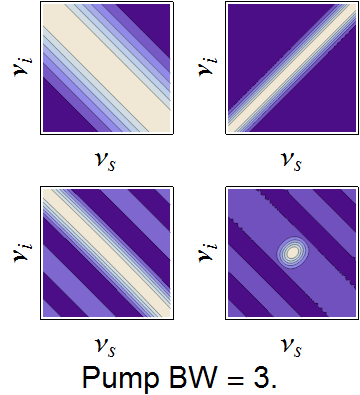
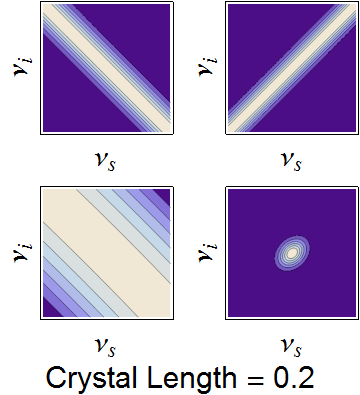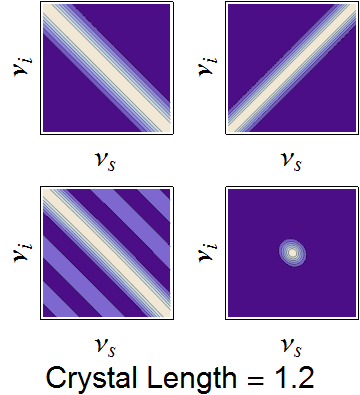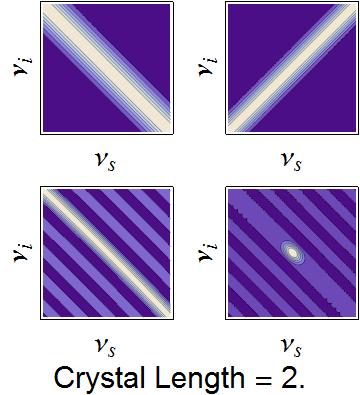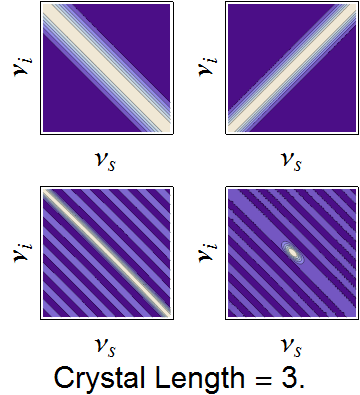
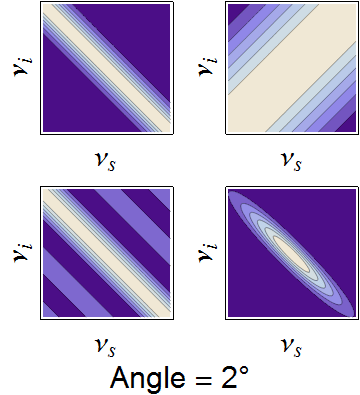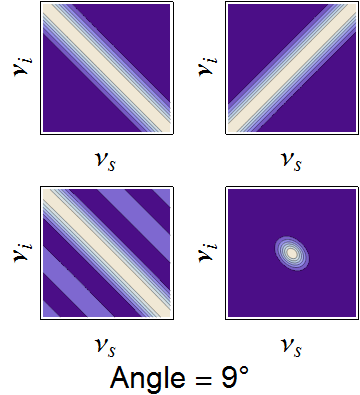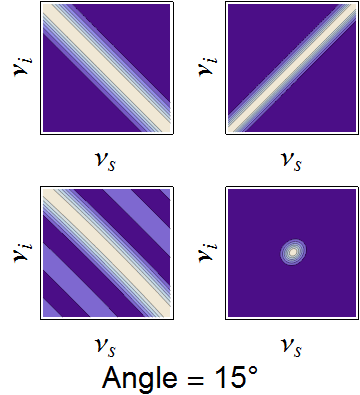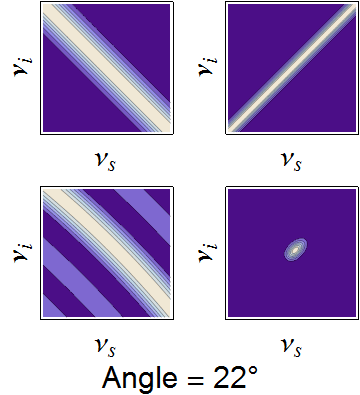
Dependence of the joint spectrum on each pump bandwidth, SPDC crystal length, and SPDC emission angle, respectively. In each image, the top-left is the pump envelope function, the to right is the transverse momentum component of the phasematching function, the bottom left is the longitudinal momentum component, and the bottom right is the joint spectral intensity -- the product of all three components
If you made it to the end and want the full story, have a look through my dissertation!
*Multiple weird tricks may be required. Void where prohibited by no-cloning and no-signaling theorems, and on Sundays.
-
Classical electromagnetic theory also allows this state, which is \(45^\circ\) or diagonal polarization. However, the Hong-Ou-Mandel effect is purely quantum mechanical and has no classical description. ↩
-
This is a consequence of requiring the beamsplitter to be a unitary operator. That is to say, for a beamsplitter acting on some input state, \(\psi_{out} = \hat{B}\psi_{in}\), we require the beamsplitter operator \(\hat{B}\) to satisfy \(\hat{B}^{*}\hat{B}=I\). ↩
-
Spontaneous parametric downconversion is a long name for a relatively simple process. We could leave it at that, but names are chosen for a reason and there’s insight in exploring this, so let’s unpack the name. SPDC is commonly referred to as just downconversion, which captures the essential nature of the process: one high-energy pump photon converts downward in energy to two “daughter” photons. The process is spontaneous because it happens randomly, stimulated by vacuum fluctuations (in contrast to an optical parametric amplifier, which amplifies an input signal beam). The use of parametric is more esoteric. In optics, the term refers to a process that leaves the state of the system unaltered (that is to say, any interactions with the nonlinear medium are instantaneous, no energy is deposited or removed, and the medium remains in the same state). The historical use of the term arises from the mathematical study of parametric oscillators, a generalization of the harmonic oscillator in which the parameters (coefficients) in the differential equation are allowed to vary in time. In the field of electronics, this is used in a parametric amplifier to amplify a signal in the presence of a pump. This also explains the origin of the terms “signal” and “idler” for the daughter photons: in an optical parametric amplifier (the optical analog of the parametric amplifier which acts on light rather than electronic signals), the signal is the input beam being amplified, while the idler is the unintended secondary beam produced to maintain energy and momentum conservation. For more on SPDC and related phenomena, check out Boyd’s Nonlinear Optics. ↩
-
This is actually the joint spectral intensity. The joint spectral amplitude is equally important, but as a complex-valued function, it is more difficult both to measure and to visualize. ↩